検索条件
全3件
(1/1ページ)
#include <stdio.h>
#include <math.h> //BSD系のC標準数学ライブラリ.
#include <gsl/gsl_sf.h> //特殊関数のヘッダファイル
#include <gsl/gsl_math.h> //数学の基本的な関数のヘッダファイル
#include <gsl/gsl_complex.h> //複素数に関する宣言や定義のヘッダファイル
#include <gsl/gsl_complex_math.h>//複素数を扱った関数のヘッダファイル
int main(void)
{
double theta = 0; //角度theta.初期値を一応設定.
double phi =0; //角度phi.初期値を一応設定.
double YY; //球面調和関数Y.spherical harmonics
//球面調和関数の直交座標系変換した値.
double xx_sh;
double yy_sh;
double zz_sh;
int l=3;
int m=0; //lとm.量子数に対応ですね.
//途中計算で作った変数.数式はTeX記法でやってます.わからない人は適当に調べてね!
//球面調和関数は,Wikipediaによれば次の式.
//Y_{l}^{m}(\theta, \phi) = (-1)^{(m+|m|)/2}
//\sqrt{ \frac{2l+1}{4\pi} \frac{(l-|m|)!}{(l+|m|)!} \,} P_l^{|m|}(\cos\theta) \, e^{im\phi}
//これを分解して見通しをよくする.
//(-1)^{(m+|m|)/2}に対応
double minus1_mm_2;
//\frac{2l+1}{4\pi}に対応
double frac_2l1_4pi;
//\frac{(l-|m|)!}{(l+|m|)!}における,分子に対応
double l_minus_abs_m;
//\frac{(l-|m|)!}{(l+|m|)!}における,分母に対応
double l_plus_abs_m;
//(\cos\theta )\exp (im\phi)に対応
double cos_theta;
double exp_imphi;
int i,j; //ループ用変数.
int stop_i=100; //ループの停止値.まあ設定する必要もない気がするけど作った….
FILE *outputdata; //データ保存用ストリーム.
FILE *outputdata_xyz; //データ保存用ストリーム.
outputdata = fopen("outputdata.txt", "w"); //データ保存ファイル,オープン
fprintf(outputdata, "#theta\tphi\tYY\n");
outputdata_xyz = fopen("outputdata_xyz.txt", "w"); //データ保存ファイル,オープン
fprintf(outputdata_xyz, "#xx_sh\tyy_sh\tzz_sh\n");
outputdata = fopen("outputdata.txt", "a");
outputdata_xyz = fopen("outputdata_xyz.txt", "a"); //データ保存ファイル,オープン
//計算用forループ.2重になっている.
for (i=1 ; i<=stop_i ; i++){
phi = phi + 0.0628;
for (j=1 ; j<=stop_i ; j++){
theta = theta + 0.0628;
minus1_mm_2 = pow(-1, (m+abs(m))/2);
frac_2l1_4pi = (2*l +1)/(M_PI_4);
l_minus_abs_m = gsl_sf_fact(l-abs(m));
l_plus_abs_m = gsl_sf_fact(l+abs(m));
//cos_theta_exp_imphi = cos(theta)*gsl_expm1();
cos_theta = cos(theta);
exp_imphi = GSL_REAL(gsl_complex_exp(gsl_complex_rect(0, m*phi)))+GSL_IMAG(gsl_complex_exp(gsl_complex_rect(0, m*phi)));
//複素数の扱いで転けた(2011年2月15日,4:49).寝ます.
//本番の計算.球面調和関数の計算.
YY=frac_2l1_4pi*sqrt(frac_2l1_4pi*(l_minus_abs_m/l_plus_abs_m))*gsl_sf_legendre_Plm(l,m,cos_theta)*exp_imphi;
//↓極座標から直交座標系に変換する.
xx_sh = YY * sin(theta) * cos(phi);
yy_sh = YY * sin(theta) * sin(phi);
zz_sh = YY * cos(theta);
//データ保存用の部分↓
fprintf(outputdata, "%f\t%f\t%f\n", theta,phi,YY);
fprintf(outputdata_xyz, "%f\t%f\t%f\n", xx_sh,yy_sh,zz_sh);
printf("iが%d回目,jが%d回目の計算結果:Y(%f,%f) = %.18e\n", i, j, theta, phi, YY);
}
theta = 0;//ここで初期化しなければthetaの値がめちゃめちゃに大きくなる.
}
fclose(outputdata); //ファイルをクローズ.
fclose(outputdata_xyz);
return 0;
}
//バグ.複素数の負値の扱いがおかしい.
//また,mを負値にするとエラーで止まる.
//だけど,それっぽいグラフは書けた.
上の値設定の状態で,出力されるグラフは次のようになります.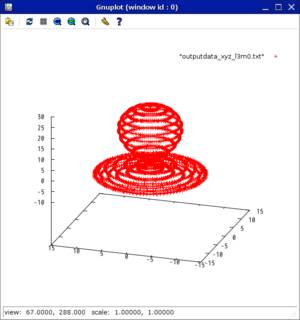
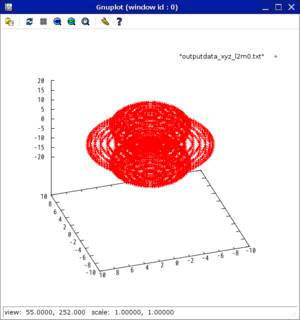
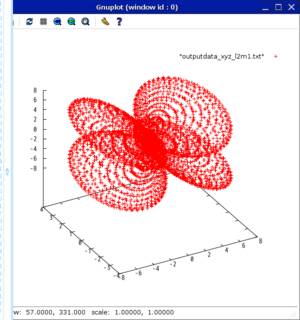
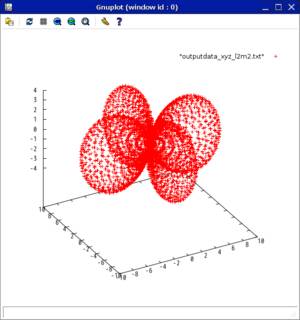
#include <stdio.h>
#include <gsl/gsl_sf.h> //特殊関数のヘッダファイル
#include <gsl/gsl_math.h> //数学の基本的な関数のヘッダファイル
int main(void)
{
double xx = -500.0; //x.初期値を一応設定.
double yy = 0; //y.初期値を設定
int i; //ループ用変数.
int stop_i=10000; //ループの停止値.まあ設定する必要もない気がするけど作った….
FILE *outputdata; //データ保存用ストリーム.
outputdata = fopen("outputdata.txt", "w"); //データ保存ファイル,オープン
fprintf(outputdata, "#xx\tyy\n");
fclose(outputdata); //データ保存ファイル,クローズ
for (i=1 ; i<=stop_i ; i++){
xx = xx + 0.1;
yy=gsl_sf_bessel_J0(xx);
outputdata = fopen("outputdata.txt", "a");
fprintf(outputdata, "%f\t%f\n", xx,yy);
printf("%d回目の計算結果:J0(%g) = %.18e\n", i, xx, yy);
fclose(outputdata);
}
return 0;
}
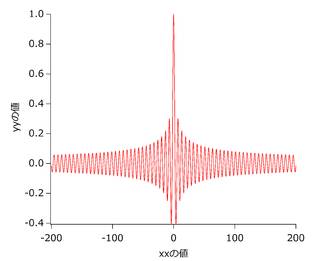
はき出したテキストファイルを範囲指定してグラフ化すると,次のようになったり.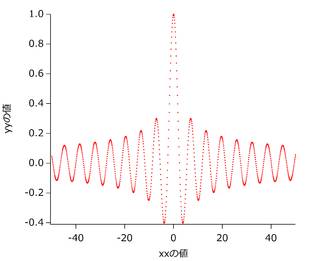
:1467,1480s/"\(.*\)"/{\1}/g
この例では,編集しているテキストファイルの1467から1480行の範囲にある,「""」で囲まれた文字列を「{}」(本当は半角の括弧)で囲むように置換している.
:237,287s/\\textbf{\(.*\)}/\\textsf{\\textbf{\1}}/g